不定方程的定义
当未知数的个数大于独立方程个数时,此类方程为不定方程。例:3x+4y=17
不定方程的解法
不定方程看似有无数组解,但结合题目条件,往往只需要求正整数解。求解不定方程的基本方法是利用带入排除法求解,但有时可能需要多次带入选项验证才能确定正确选项,其实我们可以利用一些技巧来减少带入的次数。
提示:在正整数范围内求解不定方程,通常利用整除、奇偶、尾数等进行代入排除。
1、整除法:某个未知数的系数和常数项有公约数时,可以考虑利用整除求解。
【例1】小王打靶共用了10发子弹,全部命中,都在10环、8环和5环上,总成绩为75环,则命中10环的子弹数是:
A.1发
B.2发
C.3发
D.4发
答案:B
【解析】设命中10环的有x发,命中8环的有y发,命中5环的有z发。根据题意可列方程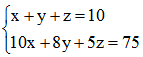 ,消去z得5x+3y=25,x的系数5和常数项25有公约数5,可以考虑利用整除求解。5x、25都能被5整除,则3y能被5整除,即y能被5整除,由于x、y的取值只能是正整数,故y=5,x=2,选择B。
,消去z得5x+3y=25,x的系数5和常数项25有公约数5,可以考虑利用整除求解。5x、25都能被5整除,则3y能被5整除,即y能被5整除,由于x、y的取值只能是正整数,故y=5,x=2,选择B。
2、奇偶性法:未知数前的系数一奇一偶,且所求未知数的系数为奇数,可以考虑利用奇偶性求解。
【例2】某单位向希望工程捐款,其中部门领导每人捐50元,普通员工每人捐20元。某部门所有人员共捐款320元,已知该部门总人数超过10人,该部门可能有几名部门领导?
A.1
B.2
C.3
D.4
答案:B
【解析】设领导有x人,普通员工y人,则50x+20y=320,化简得5x+2y=32。未知数的系数5、2一奇一偶,可以考虑利用奇偶性求解。2y是偶数,32是偶数,则5x必然是偶数,即x为偶数,排除A、C。若领导为4人,则普通员工为(320-50×4)÷20=6人,总人数没有超过10,故领导为2人。故本题选B。
3、尾数法:某一未知数的系数为5或5的倍数时,可以考虑利用尾数求解。
【例3】有271位游客欲乘大、小两种客车旅游,已知大客车有37个座位,小客车有20个座位。为保证每位游客均有座位,且车上没有空座位,则需要大客车的辆数是( )。
A.1辆
B.3辆
C.2辆
D.4辆
答案:B
【解析】设大客车需要x辆,小客车需要y辆,则37x+20y=271。y的系数20为5的倍数,可以考虑利用尾数求解。20y的尾数是0,271的尾数是1,则37x的尾数是1,结合选项可知,x=3满足题意。故本题选B。
寄语:通过以上3道题目的讲解,相信大家对于求解不定方程已经有所了解,行测中数量关系考查的题型较多,考生需要系统的学习理论知识,同时掌握一些解题技巧,在此基础之上还需要结合大量的练习做到灵活运作,从而提高解题效率。


 安徽公务员考试行测数量关系技巧
安徽公务员考试行测数量关系技巧 数量关系例题讲解
数量关系例题讲解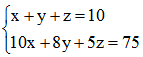 ,消去z得5x+3y=25,x的系数5和常数项25有公约数5,可以考虑利用整除求解。5x、25都能被5整除,则3y能被5整除,即y能被5整除,由于x、y的取值只能是正整数,故y=5,x=2,选择B。
,消去z得5x+3y=25,x的系数5和常数项25有公约数5,可以考虑利用整除求解。5x、25都能被5整除,则3y能被5整除,即y能被5整除,由于x、y的取值只能是正整数,故y=5,x=2,选择B。 安徽公务员考试备考
安徽公务员考试备考