基本概念
上一篇我们刚学习了现期平均数，大家对于平均数的列式和应用也应该有一些了解，那就是：平均数=总量÷份数。那么基期平均数又是什么呢?在资料分析中，一般材料中出现的统计时间我们会分为现期和基期，作为参照标准的时期称之为基期，所以求参照时期的平均数就是基期的平均数也就是我们今天所了解的内容。
基本公式
根据材料中给出的数据，当已知两个统计指标总量和份数的现期值以及对应的增长量的时候，所求为：
当已知两个统计指标总量和份数的现期值以及对应增长率的时候，所求为：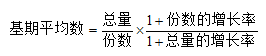
在我们做题的时候，需要注意的是，结合所求的关于基期平均数的问题，迅速找到上述公式中总量、份数指标的有关数据，代入数据，这一过程中要注意数据在公式中对应的位置。那我们可以通过几道例题来练习一下。
模拟例题
例题1、2018年，美国对华出口水果11.16万吨，相比2017年减少了4.13万吨;对华出口水果贸易总值2.69亿美元，比2017年减少了1.22亿美元。
问题：2017年美国对华出口水果均价为( )美元/吨。
解析：已知材料描述的是两个指标对华出口水果量和贸易总值关于2018年的数据，以及与2017年相比较增长带单位的量。问题求2017年美国对华水果均价，则为求基期平均数，故根据所给数据可列式为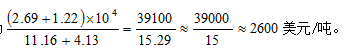
例题2、2018年北京商品住宅销售面积为526.76万平方米，同比减少13.5%;商品住宅销售额为1971.14亿元，同比减少5.1%。
问题：2017年北京商品住宅销售均价为()万元/平方米。
解析：已知材料描述的是两个指标——北京商品住宅销售面积和销售额——关于2018年的数据，以及与2017年相比较增长不带单位的率。问题求2017年北京商品房住宅均价，则为求基期平均数，故根据所给数据可列式为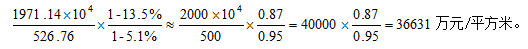
综上所述，大家对于基期平均数公式的熟练运用，重点在于对其基本概念和基本公式的理解，然后通过多做相关题目，来了解不同材料有关数据的表达方式和问题，从而实现对于求解基期平均数这一问题的快速列式。
安徽公务员考试行测资料分析题技巧
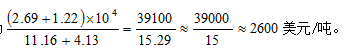
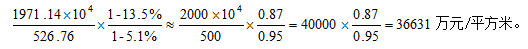
安徽公务员考试备考
